Before you start reading, I should warn you that this post has a lot of math. It’s not complicated, it’s not difficult and you really don’t need to follow the math to get the point I’m trying to make but the math is there. I only want you to see that I don’t think differently than you do but like most engineers, I want a definable set of objectives for my decisions. To achieve those objectives I will create a plan and evaluate my options. Take my recent purchase of a car as an example.

I started planning for a new car about six months ago. I had just been told my car needed new shocks and until I got new shocks, getting new tires was a bad idea and not getting new tires was a worse idea. I had some time but not much, not that I was complaining. I had already had 155,000 miles but this started the end of life calculations. New tires, brakes, shocks and if I went past July I would be paying for its annual safety inspection and registration. End of June it was. I could have waited but given the age of my car, none of the money I spent at this point would improve its trade-in value.

From that decision point I switched over to data gathering mode. Each time my company sent me on a trip I would rent a different make for comparison shopping. I think I made five trips over that period. My traveling companions were wondering why I kept getting subcompacts but for the most part we managed to fit. Data gathered and evaluated, I decided that I liked my current car best and opted to stick with the make and model.

Unlike my dishwasher and my dryer plans, this one actually came together. Both my Mother-in-law and wife were surprised that I only visited one dealer to buy my car but I only needed to make sure the new model was as good as what I had been driving. It was all a matter of planning.

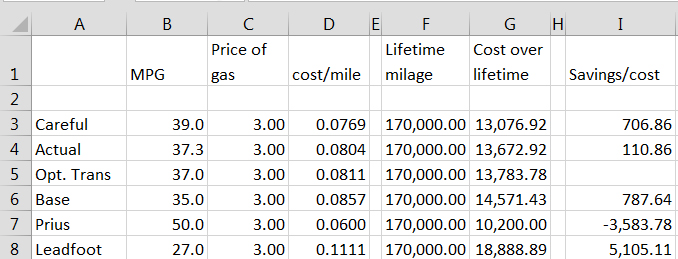
Having already decided on the make and model, I was down to a few options that could be evaluated objectively.  [Simple math warning] Let’s start with a few basic numbers. The model I was looking at offered two different transmissions. One gets 35 mpg and the other 37 mpg. If I assume $3 a gallon for gas, 35 mpg costs me 8.57 cents per mile, while 37 mpg costs me 8.11 cents per mile. That not operating costs, that’s only for the cost of gas.

By now my old car had 170,000 miles so I used that number for the comparison. 35 mpg will cost me $14,571 in gas over the life of the car, while the 37 mpg would cost me $13,784. Subtracting the numbers and the optional transmission will save me about $800 in gas over the life of the car. I can see a few faces already starting to glaze over but I find these numbers fascinating.

Although the math was very simple, I still created a spreadsheet for it. Why? Because, I’m an engineer that’s why. Having a spreadsheet allowed me to quickly evaluate a few other options. For example, a Toyota Prius gets about 50 mpg. Over the life of the car, I would save $3600 in gas costs. Since the Prius is about $5000 more than my car, I’ll stick with my Honda.

Having had my car for a few weeks now, I can report that I’m getting 37 mpg as an average. That’s not a given though, when I’m in a hurry to get someplace and start treating my new car like a Ferrari, my mileage drops all the way to 27 mpg. My wife hates it when I start driving that but now, traffic tickets aside, I can show her exactly what it costs. Going back to my charts, oops, my lead foot would cost me $5100 over the life of the car, enough for a new 3D printer and a good drone. Maybe she has a point.

Changing topics rapidly, I’m not limited to lifetime savings either. To make it easier for me to calculate, I’ll use ten cents a mile as my fuel operating cost. With a 10 gallon tank, how much cheaper does the gas have to be before it’s worth my while to drive an extra five miles? At 10 cents a mile, five miles will cause me to consume an additional $0.50 more gas. Assuming I’m almost empty, that $0.50 makes a difference of five cents a gallon my breakeven point. That’s good to know because where I live that difference is usually 10 cents a gallon. Meaning it’s worth my time to drive to the cheaper station.

Remember this is only valid if I’m getting my full 10 gallons. If I’m only filling up the 5 gallon container for the lawn mower, my savings on gas is 50 cents but I would also consume 50 cents more gas going to the farther station. That also explains why I get gas for the lawnmower at one station and gas for my car at another. It’s all in the math and the way I think.

I wrote this not to explain why I got the better transmission (the dealer was out of the other models) or why I go to different gas stations but to explain this is really the way I think. I enjoyed building the spreadsheet I used for this. I enjoyed being able to play what if with only a few numbers. By doing this I can compare gas economy and know that for my purposes, my car is the better choice.

Want to know what it’s like being married to engineer? My wife has to suffer through similar discussions all the time. She’s learned to be scarce when I break out the spreadsheets. And yet I still find the numbers exciting, that’s what it’s like being married to an engineer.

© 2015 – 2019, Byron Seastrunk. All rights reserved.